Varianza y desviación estándar
La varianza y la desviación estándar indican si los valores se encuentran más o menos próximos a las medidas de posición.
Para Malhotra (2008), la varianza es una “técnica estadística que sirve para examinar las diferencias entre las medias de dos o más poblaciones” (p. 505). La formula de la varianza es:
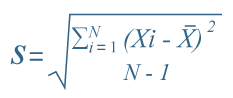
La desviación estándar es simplemente la raíz cuadrada positiva de la varianza.
Para comprender el concepto de la varianza y de la desviación estándar, a manera de ejemplo, si una persona gerente de una empresa de alimentos desea saber qué tanto varían los pesos de los empaques (en gramos) de sus productos, selecciona al azar cinco unidades de ellos para pesarlos, y se obtuvieron los siguientes pesos en gramos: 490, 500, 510, 515 y 520, respectivamente.
Dados estos datos, lo primero que se calcula es la media de esos datos:
(490 + 500 + 510 + 515 + 520) / 5 = 507
La varianza se calcula de la siguiente manera:
(490-507)2 + (500-507)2 + (510-507)2 + (515-507)2 + (520-507)2/ 5-1 = 145
Por lo tanto, la desviación estándar sería: √145
= 12,04
Con estos datos se llega a la conclusión de que el peso promedio de los empaques es de 507 gramos, con una tendencia a variar por debajo o por encima de dicho peso en 12 gramos. Esta información le permite a quienes toman decisiones en la empresa, determinar cuánto es el promedio de pérdidas causado por el exceso de peso en los empaques, y le da las bases para tomar los correctivos necesarios en el proceso de empacado.